时间过得真快啊,转专业的第一个学期也已过去大半,学到了不少东西。但现在有种眼高手低的感觉,又有种无力感,要学的东西有很多,学校的课程不能落下,又怕基础不牢固
在这边立个flag吧,寒假学java,wxml,leetcode刷300题,暂且这样~
以下是正文
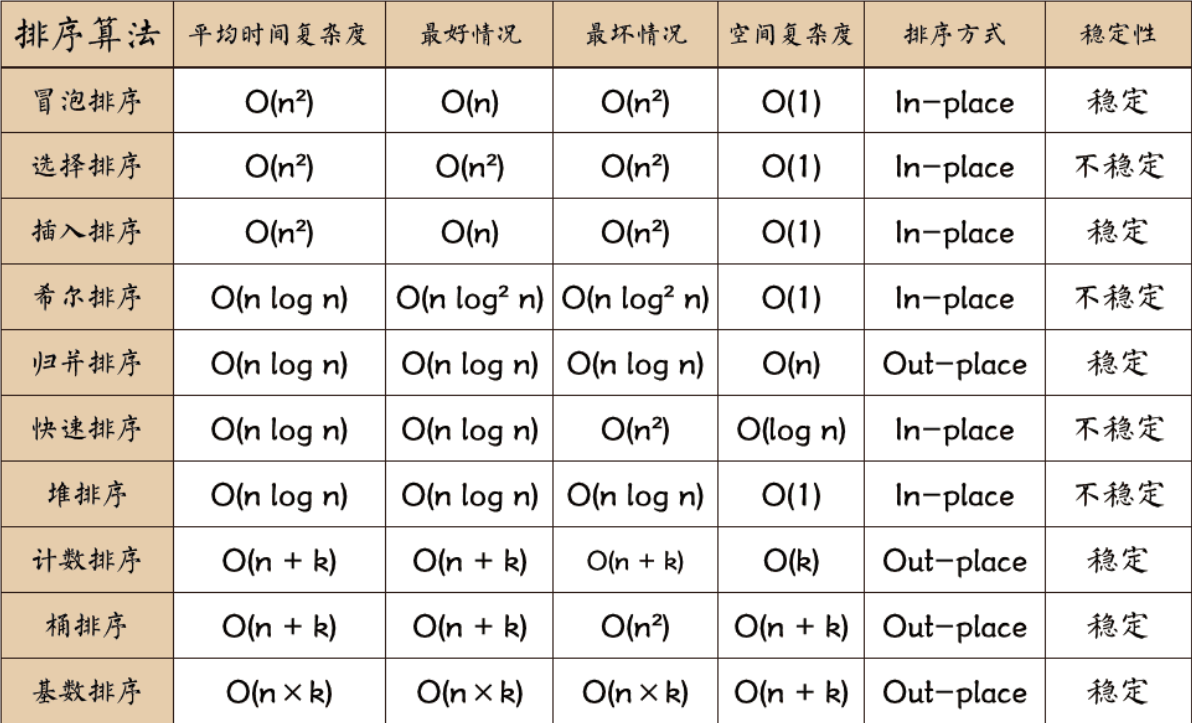
今天讨论几种经典排序😄 ,主要是书上的代码又臭又长😂 ,虽然说,有几个写的还是不错的😆~
冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
//冒泡
void bubSort(int arr[], int length) {
int flag = 1;//优化:若flag不为1;那么说明没有交换,数组有序
while (length-- && flag) {
flag = 0;
for (int i = 0; i < length; i++) {
if (arr[i] > arr[i + 1]) {
flag = 1;
int tmp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = tmp;
}
}
}
}
选择排序
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
//选择
void sortArr(int arr[], int length) {
for (int i=0;i<length;i++)
{
int min = i;
for (int j = i+1; j < length; j++) {
if (arr[i] > arr[j]) {
min = j;
}
}
int tmp = i;
arr[i] = arr[min];
arr[min] = arr[tmp];
}
}
插入排序
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
//插入
void InsertArr(int arr[], int length) {
for (int i = 1; i < length; i++) {
for (int j = i; j > 0 && arr[j]<arr[j-1]; j--) {
int tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
}
}
}
希尔排序
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
希尔排序是建立在插入排序的基础上进行优化的排序算法,所以希尔排序又叫做优化版的插入排序。
//希尔(优化版插入)在数据量大的时候速度更快
void shellArr(int arr[], int length) {
int h = 4;
int t = length / 3;
/*while (h < t) {
h = 3 * h + 1;
}*/
while (h>=1)
{
for (int i = h; i < length; i++) {
for (int j = i; j > 0 && arr[j] < arr[j - h]; j-=h) {
int tmp = arr[j];
arr[j] = arr[j - h];
arr[j - h] = tmp;
}
}
h /= 2;//h/=3;
}
}
快速排序
-
从数列中挑出一个元素,称为 “基准”(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
void quicksort(int arr[],int left, int right)
{
if (left >= right) {
return;
}
int i = left;
int j = right;
int povit = arr[i];
while (i<j)
{
while (i<j && arr[j]>=povit) {
j--;
}
arr[i] = arr[j];
while (i<j && arr[i]<=povit)
{
i++;
}
arr[j] = arr[i];
}
arr[i] = povit;
if (left < i - 1) {
quicksort(arr, left, i - 1);
}
if (i + 1 < right) {
quicksort(arr, i + 1, right);
}
}
void swap(int arr[], int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
void quicksort2(int arr[], int left, int right) {
if (left >= right) {
return;
}
int pivot = arr[left];
int i = left + 1;
int j = left + 1;
while (j<=right) {
if (arr[j] < pivot) {
swap(arr, i, j);
i++;
}
j++;
}
swap(arr, left, i - 1);
quicksort2(arr, left, i - 2);
quicksort2(arr, i, right);
}
归并排序
-
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
-
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
-
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
-
重复步骤 3 直到某一指针达到序列尾;
-
将另一序列剩下的所有元素直接复制到合并序列尾。
//归并排序,假设两个数组都有序
void mergesort(int a[], int alen,int b[], int blen, int* tmp) {
int i = 0, j = 0, k = 0;
while (i<alen && j<blen)
tmp[k++] = a[i] < b[j] ? a[i++] : b[j++];
while (i<alen)
tmp[k++] = a[i++];
while (j < blen)
tmp[k++] = b[j++];
}
//归并排序
void mergesort1(int arr[],int l, int r,int * c) {
if (l == r) return;
int m = (l + r) / 2;
mergesort1(arr, l, m,c);
mergesort1(arr, m + 1, r,c);
int p1 = l, p2 = m + 1, tot = 0;
while (p1<=m && p2<=r)
{
c[++tot] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1<=m)
{
c[++tot] = arr[p1++];
}
while (p2 <= r)
{
c[++tot] = arr[p2++];
}
for (int i = 1; i <= tot; i++) {
arr[i + l - 1] = c[i];
}
}
计数排序
初始化临时数组 tmp: tmp 数组用于统计每个元素的出现次数,初始化为全零。
复制原始数组 arr 到临时数组 brr: 这里创建了一个 brr 数组,用于保存原始数组的副本。
计数排序过程: 使用 tmp 数组统计每个元素的出现次数。
根据计数排序结果更新原始数组 arr: 通过循环遍历 tmp 数组,将元素按照计数结果还原到原始数组 arr。
实现排序的稳定性: 通过前缀和的方式,计算出每个元素在排序后数组中的位置,并存储在数组 r 中。
输出排序后的位置信息: 最后通过循环输出数组 r 中的元素,即表示每个元素在排序后数组中的位置。
//计数排序
int tmp[100] = { 0 };
void countsort(int arr[], int length) {
int brr[Maxsize];
for (int i = 0; i < length; i++) {
brr[i] = arr[i];
}
for (int i = 0; i < length; i++) {
tmp[arr[i]]++;
}
for (int i=0,j = 0; i < 100; i++) {
for (int k = 0; k < tmp[i];k++) {
arr[j++] = i;
}
}
//原来的数组的数在现在数组的哪个位置,实现排序的稳定性
// 排完后在第几位,相同数字,序号小的在前面
//先做一个前缀和
int c[1000] = { 0 };
int r[1000];
for (int i = 1; i < 100; i++) {
tmp[i] += tmp[i - 1];
}
for (int i = length - 1; i >= 0; --i) {
r[i] = tmp[brr[i]]--;
}
for (int i = 0; i < length; i++) {
printf("%d ", r[i]);
}
printf("\n");
}
基数排序
假设现在我们已经排完了第i个及以后的关键字,现在要拍i-1个关键字,这里其实是一个双关键字排序(第一关键字是原来的第i-1个关键字,第二个关键字是原来的第i个及以后的关键字的rank)
我们只要把数字按第i个及以后的关键字从小到大的顺序放到数组里,在做一次计数排序就好了。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<string.h>
int n/*几个数字*/,m = 10/*数字最多几位*/,a[10001], s[10001]/*排完后在第几位,相同数字,序号小的在前面*/,v[10001]/*第一关键字*/, rank[10001]/*排完后在第几位,相同数字,序号小的在前面*/,c[10];//做计数排序的桶
void countingsort() {
memset(c, 0, sizeof(c));
for (int i = 1; i <= n; i++) {
++c[v[i]];//c[当前关键字],将其放入桶中
}
for (int i = 1; i <= 9; i++) {//前缀和
c[i] += c[i - 1];
}
for (int i = n; i >= 1; --i) {
rank[s[i]] = c[v[s[i]]]--;//v[s[i]]表示当前关键字v的情况下,在s[i]这个位置。这句话表示,在s[i]这个位置在原数组中的位置是c[v[s[i]]]
}
for (int i = 1; i <= n; i++) {
s[rank[i]] = i;//已知rank是已经排完的表示从v[0,10],在原数组中的位置。s[rank[i]] 表示排序后数组中排名为 rank[i] 的位置上的元素。=i 表示将原始数组中的第 i 个元素放置到相应的位置上。这行代码的目的是将排完序的数组 s 的第 rank[i] 个位置上的值设置为 i。
}
}
void radixsort() {
for (int i = 0; i <= n; i++) {
s[i] = i;//当前位置
}
int x = 1;//用来帮我们统计当前变量
for (int i = 0; i <= m; i++, x *= 10) {//x*10表示1,10,100
for (int j = 1; j <= n; j++) {
v[j] = a[j] / x % 10;//当前关键字
}
countingsort();
}for (int i = 1; i <= n; i++) {
printf("%d ", a[s[i]]);
}
printf("\n");
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
radixsort();
return 0;
}
完整代码
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define Maxsize 10
void initArr(int arr[], int length) {
for (int i = 0; i < length; i++) {
arr[i] = rand() % 100;
}
}
void showArr(int arr[], int length) {
for (int i = 0; i < length; i++) {
printf("%d ", arr[i]);
}
printf("\n-----------------------\n");
}
//冒泡
void bubSort(int arr[], int length) {
int flag = 1;//优化:若flag不为1;那么说明没有交换,数组有序
while (length-- && flag) {
flag = 0;
for (int i = 0; i < length; i++) {
if (arr[i] > arr[i + 1]) {
flag = 1;
int tmp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = tmp;
}
}
}
}
//选择
void sortArr(int arr[], int length) {
for (int i=0;i<length;i++)
{
int min = i;
for (int j = i+1; j < length; j++) {
if (arr[i] > arr[j]) {
min = j;
}
}
int tmp = i;
arr[i] = arr[min];
arr[min] = arr[tmp];
}
}
//插入
void InsertArr(int arr[], int length) {
for (int i = 1; i < length; i++) {
for (int j = i; j > 0 && arr[j]<arr[j-1]; j--) {
int tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
}
}
}
//希尔(优化版插入)在数据量大的时候速度更快
void shellArr(int arr[], int length) {
int h = 4;
int t = length / 3;
/*while (h < t) {
h = 3 * h + 1;
}*/
while (h>=1)
{
for (int i = h; i < length; i++) {
for (int j = i; j > 0 && arr[j] < arr[j - h]; j-=h) {
int tmp = arr[j];
arr[j] = arr[j - h];
arr[j - h] = tmp;
}
}
h /= 2;//h/=3;
}
}
void quicksort(int arr[],int left, int right)
{
if (left >= right) {
return;
}
int i = left;
int j = right;
int povit = arr[i];
while (i<j)
{
while (i<j && arr[j]>=povit) {
j--;
}
arr[i] = arr[j];
while (i<j && arr[i]<=povit)
{
i++;
}
arr[j] = arr[i];
}
arr[i] = povit;
if (left < i - 1) {
quicksort(arr, left, i - 1);
}
if (i + 1 < right) {
quicksort(arr, i + 1, right);
}
}
void swap(int arr[], int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
void quicksort2(int arr[], int left, int right) {
if (left >= right) {
return;
}
int pivot = arr[left];
int i = left + 1;
int j = left + 1;
while (j<=right) {
if (arr[j] < pivot) {
swap(arr, i, j);
i++;
}
j++;
}
swap(arr, left, i - 1);
quicksort2(arr, left, i - 2);
quicksort2(arr, i, right);
}
//归并排序,假设两个数组都有序
void mergesort(int a[], int alen,int b[], int blen, int* tmp) {
int i = 0, j = 0, k = 0;
while (i<alen && j<blen)
tmp[k++] = a[i] < b[j] ? a[i++] : b[j++];
while (i<alen)
tmp[k++] = a[i++];
while (j < blen)
tmp[k++] = b[j++];
}
//归并排序
void mergesort1(int arr[],int l, int r,int * c) {
if (l == r) return;
int m = (l + r) / 2;
mergesort1(arr, l, m,c);
mergesort1(arr, m + 1, r,c);
int p1 = l, p2 = m + 1, tot = 0;
while (p1<=m && p2<=r)
{
c[++tot] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1<=m)
{
c[++tot] = arr[p1++];
}
while (p2 <= r)
{
c[++tot] = arr[p2++];
}
for (int i = 1; i <= tot; i++) {
arr[i + l - 1] = c[i];
}
}
//计数排序
int tmp[100] = { 0 };
void countsort(int arr[], int length) {
int brr[Maxsize];
for (int i = 0; i < length; i++) {
brr[i] = arr[i];
}
for (int i = 0; i < length; i++) {
tmp[arr[i]]++;
}
for (int i=0,j = 0; i < 100; i++) {
for (int k = 0; k < tmp[i];k++) {
arr[j++] = i;
}
}
//原来的数组的数在现在数组的哪个位置,实现排序的稳定性
// 排完后在第几位,相同数字,序号小的在前面
//先做一个前缀和
int c[1000] = { 0 };
int r[1000];
for (int i = 1; i < 100; i++) {
tmp[i] += tmp[i - 1];
}
for (int i = length - 1; i >= 0; --i) {
r[i] = tmp[brr[i]]--;
}
for (int i = 0; i < length; i++) {
printf("%d ", r[i]);
}
printf("\n");
}
int main()
{
srand((unsigned int)time(NULL));
int arr[Maxsize];
int c[2000];
/*initArr(arr, Maxsize);
showArr(arr, Maxsize);
bubSort(arr, Maxsize);
showArr(arr, Maxsize);
sortArr(arr, Maxsize);
showArr(arr, Maxsize);
InsertArr(arr, Maxsize);
showArr(arr, Maxsize);
shellArr(arr, Maxsize);
quicksort2(arr, 0, Maxsize - 1);
showArr(arr, Maxsize);*/
initArr(arr, Maxsize);
showArr(arr, Maxsize);
/*mergesort1(arr, 0, Maxsize - 1, c);*/
countsort(arr, 10);
showArr(arr, Maxsize);
//归并排序使用该数组
/*int a[5] = { 1,3,5,7,9 };
int b[5] = { 0,2,4,6,8 };
int tmp[10];
mergesort(a, 5, b, 5, tmp);
showArr(tmp, 10);*/
return 0;
}